Multicomplex number

In mathematics, the multicomplex number systems C_n are defined inductively as follows: Let C₀ be the real number system. For every n > 0 let i_n be a square root of minus one, that is, an imaginary number. Then 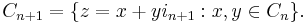$C_{n%2B1} = \lbrace z = x %2B y i_{n%2B1}�: x,y \in C_n \rbrace .$ In the multicomplex number systems one also requires when n ≠ m that 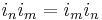$i_n i_m = i_m i_n$ (commutative property). Then C₁ is the complex number system, C₂ is the bicomplex number system, C₃ is the tricomplex number system of Corrado Segre, and C_n is the multicomplex number system of order n.

Each C_n forms a Banach algebra. G. Bayley Price has written about the function theory of multicomplex systems, providing details for the bicomplex system C₂.

The multicomplex number systems are not to be confused with Clifford numbers (elements of a Clifford algebra), since Clifford's square roots of minus one anti-commute (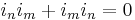 $i_n i_m %2B i_m i_n = 0$ for Clifford). Furthermore, the multicomplex systems differ from the n-complex numbers introduced by Silviu Olariu in 2002. In particular, Olariu's tricomplex numbers differ from Segre's tricomplex numbers C₃ defined above.

With respect to subalgebra C_k, k = 0, 1, ... n−1, the multicomplex system C_n is of dimension 2^n−k over C_k.

References

G. Baley Price (1991) An Introduction to Multicomplex Spaces and Functions, Marcel Dekker.
Corrado Segre (1892) "The real representation of complex elements and hyperalgebraic entities" (Italian), Mathematische Annalen 40:413–67 (see especially pages 455–67).